Received 19 June 2017; Revised 9 October 2017, 25 January 2018; Accepted 31 January 2018
Agnieszka Lipieta, Ph. D. , Cracow University of Economics, Faculty of Finance and Law, Department of Mathematics, Rakowicka 27, 31 - 510 Cracow, Poland, email: alipieta@uek. krakow,pl.
Andrzej Malawski, Professor, Cracow University of Economics, Faculty of Finance and Law, Department of Mathematics, Rakowicka 27, 31 - 510 Cracow, Poland. He passed away in 2016.
Abstract
The paper extends the research program of modeling the Schumpeterian vision of innovative development in the framework of the Arrow-Debreu theory of general equilibrium. To study changes in the production sector, as well as in the whole economy, the concept of extension of the systems under study is introduced. It enables us to model the mechanisms of Schumpeterian evolution in the conceptual apparatus of Hurwicz’s theory of economic mechanisms.
The paper is aimed at expanding our previous studies into two new directions. First, we establish the conditions sufficient for improving positions of various groups of agents such as producers, innovators, consumers, etc., under the price or qualitative mechanism regime. Second, to compare mechanisms of Schumpeterian evolution, we respect the logic of this process which is determined by innovative, as well as adaptive, equilibrium changes in the evolving economy under consideration. Consequently, we formulate two different criteria in our comparative analysis based, on the one hand, on the index of the distance between two innovative extensions of the given economic system and, on the other hand, on the increase in wealth of the given set of agents.
The motivations of innovators, and the reason for which innovations are adopted into the producers’ and consumers’ plans of action, are also precisely explained in the paper. The results of our theoretical research can be useful in economic analyses, among others, in the case of the lack of the sufficient access to statistical data.
Due to both the formal conceptual apparatus of the general equilibrium theory and Hurwicz’s approach to the problem of designing economic mechanisms, the paper takes the form of an axiomatic deductive system of mathematical theorems interpreted in the language of economics.
Keywords: Schumpeterian evolution, mechanisms, designing mechanisms, Debreu economy.INTRODUCTION
Joseph Schumpeter distinguished two forms of economic life: the circular flow and economic development based on innovations (see Schumpeter, 1934). The circular flow resembles the “blood circulation in a living organism” and is interpreted as the stagnation of economic life. Economic development, driven by innovators, means a spontaneous and discontinuous change in the channels of the circular flow and usually implies the disturbance of equilibrium. During economic development, two tendencies in the production sphere are observed: innovation creation and the elimination of existing products or organizational structures and their replacement by new ones. Finally, it moves the system back to a new stationary state, where previous innovations have been absorbed in an equilibrated system. The analysis of mechanisms of economic evolution was at the core of Joseph Schumpeter’s interest.
The paper is aimed at expanding our previous studies into two new directions. First, we establish the conditions sufficient for improving positions of various groups of agents such as producers, innovators, consumers, etc., under the price or qualitative mechanism regime. Second, to compare mechanisms of Schumpeterian evolution, we respect the logic of this process which is determined by innovative, as well as adaptive, equilibrium changes in the evolving economy under consideration. Consequently, we suggest two different criteria in our comparative analysis based, on the one hand, on the index of the distance between two innovative extensions of the given economic system and, on the other hand, on the increase in wealth of the given set of agents.
Finally, it should be emphasized that from the methodological viewpoint we go beyond the perfect rationality paradigm in our modeling, because economic agents are not able to perform their optimal plans of actions in out-of-equilibrium states. To model such stages of evolutionary process, we define and analyze economic systems labeled as quasi-systems.
This paper consists of six parts. In the second part, the literature review is presented, while in the third part, the research method used in the paper is characterized. In the fourth part the basic model, namely the private ownership economy with almost all inactive agents, as well as various kinds of extensions of subsystems of the considered economy, and extensions of the economy as a whole, are defined. In the fourth part, the reader can also find the short characteristics of Hurwicz’s economic mechanisms as well as the comparative analysis of the innovative evolution and the adopting mechanisms, respectively. The fifth part is devoted to discussion, and the sixth part contains the conclusions. Due to the formal conceptual apparatus of the general equilibrium theory, as well as Hurwicz’s approach to the problem of designing economic mechanisms, the paper takes the form of an axiomatic deductive system of mathematical theorems interpreted in the language of economics.
LITERATURE REVIEW
The paper extends the research program of modeling the Schumpeterian vision of innovative development in the Arrow-Debreu theory of general equilibrium (cf. Malawski, 2005, 2008; Malawski & Woerter, 2006; Ciałowicz & Malawski, 2011; Malawski, 2013). The core of this set-up is based on modeling the two fundamental forms of economic life distinguished by Schumpeter (1934), namely the circular flow and economic development by specific extensions of the production and consumption systems being the part of the Debreu private ownership economy, so that the analysis includes static as well as dynamic forms. Moreover, this research program has been recently combined (see Lipieta & Malawski, 2016; Lipieta, 2013) with Hurwicz’s theory of economic mechanism (see for instance Hurwicz & Reiter, 2006).
At the same time, the current neo-Schumpeterian studies suggest (Hanusch & Pyka, 2007; Andersen, 2009) that the Schumpeterian innovative evolution is governed by two different kinds of mechanisms. First, quantitative, price mechanisms to determine the prices and quantities of goods in the state of Walrasian equilibrium corresponding to the circular flow, and, second, qualitative mechanisms typical for economic development explaining the role of innovations.
Indeed, Andersen (2009) identifies two opposing evolutionary mechanisms: first, the mechanism of innovation which moves the economic system from a stationary state to its maximally disequilibrated state; Second, the mechanism of adaptation to move the system back to a new stationary state, where previous innovations have been absorbed in an equilibrated system of economic routines.
Similarly, transition from the circular flow to economic development can be characterized as follows (Hanusch & Pyka, 2007): “It is no longer price competition only, but following his ideas of development, quality competition, driven by innovations and imitations of economic actors, takes over the leading role. In other words, profit opportunities are signaled not exclusively by market prices but also by creativity and daringness of entrepreneurial actors who change the relative scarcity in an economic system”.
This analysis of Schumpeterian evolution mechanisms, presented above, suggests that the mechanisms under study can be classified into two categories: price mechanisms corresponding to circular flow and qualitative mechanisms based on innovations. However, our general, more rigorous setting (see also Lipieta & Malawski, 2016; Lipieta, 2013) implies that it is difficult to preserve this dichotomy and a variety of economic mechanisms should be taken into account. The main premise in this context is based on our viewpoint that the consequences of innovative changes contribute to more diversified results. Specifically, this variety of qualitative mechanisms concerns the agents whose positions get better off. Thus we can distinguish qualitative mechanism with respect to the given set of agents, for example, the set of innovators or all producers.
RESEARCH METHOD
The axiomatic method is the main method used in the paper. The axiomatic method in economy was initiated in the 1930s, during the studies on the problem of the existence of the Walras equilibrium, especially by Wald and Neumann. After that, the axiomatic method appeared respective, natural and useful, especially in theoretical economics. Using the rationality assumption of behavior of economic agents and the principle ceteris paribus, it lets us isolate the objects under study from the rest of the world. We can find axiomatic models in, for instance, the theory of general equilibrium, social choice theory, and the theory of mechanism design. These theoretical models play an important role also in empirical economics, indicating the objects and variables worth being empirically verified.
Generally, we can say that the mathematical methods play the role of mental experiments to allow us the analysis of economic processes. Some of our results have the form of theorems with rigorous proofs.
ANALYSIS
The private ownership economy with almost all inactive agents
In the process of evolution of an economy, some agents can enter or exit the market. Hence, in modeling the structure of Schumpeterian evolution, it is convenient to consider the economy with a countable number of agents (compare to Lipieta, 2013). Firstly, the production sector of the economy will be defined. Let
- 𝐵 = (𝑏𝑗)𝑗∈ℕ - be a countable set of producers,
- 𝑦: 𝐵 ∋ 𝑏𝑗 → 𝑌𝑏𝑗 ⊂ ℝℓ - be a correspondence of production sets, which to every producer 𝑏𝑗 assigns a non-empty production set 𝑦(𝑏𝑗) = 𝑌𝑏𝑗 ⊂ ℝℓ of the producer’s feasible production plans, where
∃ 𝑛 ∈ ℕ ∀𝑗 > 𝑛 𝑦(𝑏𝑗) ≝ {0},
- 𝑝 ∈ ℝℓ be a price vector.
Definition 1. The two-range relational system
𝑃𝑞 = (𝐵,ℝℓ ;𝑦,𝑝),
is called the quasi-production system. The producer 𝑏𝑗 for which 𝑦(𝑏𝑗) = {0} is called the inactive producer, while the producer for which 𝑦(𝑏𝑗) ≠ {0} is called the active one.
The idea of the set of inactive agents simplifies comparing changes in the system under study at different points of time. Especially, it enables us to consider the potential future producers in the initial system 𝑃𝑞 as well as the producers which will stop, after some time, their activities in the market.
Definition 2. If 𝑃𝑞 = (𝐵,ℝℓ ;𝑦,𝑝) is the quasi-production system in which for given price vector 𝑝 ∈ ℝℓ
∀ 𝑏 ∈ 𝐵 𝜂𝑏 (𝑝) ≝ {𝑦𝑏∗ ∈ 𝑌𝑏 : 𝑝 ∘ 𝑦 𝑏∗ = max{𝑝 ∘ 𝑦𝑏 : 𝑦𝑏 ∈ 𝑌𝑏}} ≠ ∅,
then
- 𝜂: 𝐵 ∋ 𝑏 → 𝜂𝑏(𝑝) ⊂ ℝℓ is called the correspondence of supply at price system 𝑝,
- 𝜋: 𝐵 ∋ 𝑏 → 𝜋(𝑏) = 𝑝 ∘ 𝑦 𝑏∗ ∈ ℝ is called the maximal profit function at price system 𝑝, where 𝑦𝑏∗ ∈ 𝜂𝑏(𝑝) for every 𝑏 ∈ 𝐵,
- the quasi-production system 𝑃𝑞 is called the production system and denoted by
𝑃𝑞 = 𝑃 = (𝐵,ℝℓ ;𝑦,𝑝,𝜂,𝜋).
Every element 𝑦𝑏∗ of the set 𝜂𝑏(𝑝) is called the optimal plan of producer 𝑏.
The “quasi-type” of production systems enables us to model the production sector of an economy under a bounded rationality assumption. This is because, in the quasi-production system, the aims of producers are not specified in contrast to the production system (compare to Def. 1 and 2), where producers maximize profits at given prices and technologies. Hence, to keep up the spirit of Schumpeterian thinking, innovations and structural changes of the production sector of an economy are modeled in the quasi-production systems (compare to Lipieta, 2013).
Similarly, a quasi-consumption system is defined. Let
- 𝐴 = (𝑎𝑖)𝑖∈ℕ be a countable set of consumers,
- 𝑃𝑟𝑒𝑓 ⊂ ℝℓ × ℝℓ be the family of all preference relations in ℝℓ,
- 𝜒: 𝐴 ∋ 𝑎𝑖 → 𝜒(𝑎𝑖) = 𝑋𝑎𝑖 ⊂ ℝℓ be a correspondence of consumptions sets which to every consumer 𝑎𝑖 assigns a nonempty consumption set
𝜒(𝑎𝑖) = 𝑋𝑎𝑖 being a subset of the commodity space ℝℓ and representing the consumer’s feasible consumption plans with respect to his psycho-physical structure; moreover
∃ 𝑚 ∈ ℕ ∀𝑖 > 𝑚 𝜒(𝑎𝑖) ≝ {0},
- 𝜖: 𝐴 ∋ 𝑎𝑖 → 𝜖(𝑎𝑖) ∈ 𝜒(𝑎𝑖) be an initial endowment mapping,
- 𝜀 ⊂ 𝐴 × (ℝℓ × ℝℓ) be a correspondence, which to every consumer
𝑎 ∈ 𝐴 assigns a preference relation ≼𝑎 from set 𝑃𝑟𝑒𝑓 restricted to set
𝜒(𝑎) × 𝜒(𝑎),
- 𝑝 ∈ ℝℓ be a price vector.
Definition 3. The three-range relational system
𝐶𝑞 = (𝐴, ℝℓ ,𝑃𝑟𝑒𝑓; 𝜒,𝜖,𝜀,𝑝)
is called the quasi-consumption system. The consumer 𝑎𝑖 for which
𝜒(𝑎𝑖) = {0} is called the inactive consumer, while the consumer for which
𝜒(𝑎𝑖) ≠ {0} is called the active one.
Definition 4. If 𝐶𝑞 = (𝐴, ℝℓ, 𝑃𝑟𝑒𝑓; 𝜒,𝑒,𝜀,𝑝) is the quasi-consumption system in which for price vector 𝑝 ∈ ℝℓ and for every 𝑎 ∈ 𝐴
𝛽𝑎(𝑝) = {𝑥 ∈ 𝜒(𝑎): 𝑝 ∘ 𝑥 ≤ 𝑝 ∘ 𝑒(𝑎)} ≠ ∅.
𝜑𝑎(𝑝) = {𝑥𝑎∗ ∈ 𝛽(𝑎): ∀𝑥𝑎 ∈ 𝛽(𝑎) 𝑥𝑎 ≼𝑎 𝑥𝑎∗, ≼ 𝑎 ∈ 𝑃𝑟𝑒𝑓} ≠ ∅,
then
- 𝛽: 𝐴 ∋ 𝑎 → 𝛽𝑎(𝑝) ⊂ ℝℓ is the correspondence of budget sets at price system 𝑝,
- 𝜑: 𝐴 ∋ 𝑎 → 𝜑𝑎(𝑝) ⊂ ℝℓ is the demand correspondence at price system 𝑝,
- the quasi-consumption system 𝐶𝑞 is called the consumption system and denoted by 𝐶 = (𝐴, ℝℓ ,𝑃𝑟𝑒𝑓; 𝜒,𝑒,𝜀,𝑝,𝛽,𝜑).
Every element 𝑥𝑎∗ of the set 𝜑𝑎(𝑝) is called the optimal plan of consumer 𝑎.
The “quasi-type” of consumption system allows a situation where there is no upper bound on the budget set for the preference relation of a consumer. However, we assume, according to the rationality assumption, that if there is a consumption plan maximizing the preference relation of consumer 𝑎 on his budget set, then consumer 𝑎 just realizes his best plan (one of his best plans). Now, we can assume the following definition:
Definition 5. The relational system
ℇ𝑞 = (ℝℓ ,𝑃𝑞 ,𝐶𝑞 ,𝜃,𝜔)
where
- 𝑃𝑞 = (𝐵, ℝℓ ;𝑦,𝑝) is the quasi-production system,
- the mapping 𝜃: 𝐴 × 𝐵 → [0,1] satisfies
𝜃(𝑎𝑖 ,𝑏𝑗) = 0 if 𝑖 > 𝑚 or 𝑗 > 𝑛, ∀𝑏 ∈ 𝐵 ∑𝑎∈𝐴 𝜃(𝑎,𝑏) = 1,
- 𝐶𝑞 = (𝐴, ℝℓ , 𝑃𝑟𝑒𝑓; 𝜒, 𝜖, 𝜀, 𝑝) is the quasi-consumption system,
- 𝜖(𝑎𝑖) ∈ ℝℓ for 𝑖 ∈ ℕ, 𝜖(𝑎𝑖) ≝ 0 ∈ ℝℓ for 𝑖 > 𝑚,
∑𝑎∈𝐴 𝜖(𝑎) = 𝜔
is called the private ownership economy with almost all inactive agents. If 𝑃𝑞 is the production system (𝑃𝑞 = 𝑃) and 𝐶𝑞 is the consumption system (𝐶𝑞 = 𝐶), then the private ownership economy with almost all inactive agents ℇ𝑞 will be called the Debreu economy.
If ℇ𝑞 is the Debreu economy, then it will be denoted by ℇ𝑞 = ℇ𝑝 where ℇ𝑝 = (ℝℓ ,𝑃,𝐶,𝜃,𝜔).
The private ownership economy with almost all inactive agents operates as follows. Let a price vector 𝑝 ∈ ℝℓ be given. Every active producer 𝑏 realizes a production plan 𝑦̃𝑏 ∈ 𝑦(𝑏). It is assumed that every inactive producer 𝑏𝑗 realizes plan 𝑦̃ 𝑏𝑗 = 0 ∈ ℝℓ (his activity is reduced to zero production plan). The profit of each producer 𝑏, by realization of the plan 𝑦̃𝑏 , is divided among all consumers according to function 𝜃. Hence, the expenditure (wealth) of every consumer 𝑎 cannot be greater than the value
𝑤(𝑎) = 𝑝 ∘ 𝜖(𝑎)+∑𝑏∈𝐵 𝜃(𝑎,𝑏)∙ 𝑝 ∘ 𝑦̃𝑏 .
So the budget set of every consumer 𝑎 at price system 𝑝 is of the form
𝛽𝑎(𝑝) = {𝑥 ∈ 𝜒(𝑎): 𝑝 ∘ 𝑥 ≤ 𝑤(𝑎)}.
In this situation, if 𝛽𝑎(𝑝) ≠ ∅ and 𝜑𝑎(𝑝) ≠ ∅ at given price system 𝑝 (see Def. 4), then consumer 𝑎 chooses his consumption plan 𝑥̃𝑎 = 𝑥𝑎∗ ∈ 𝜑𝑎(𝑝) ⊂ 𝜒(𝑎) maximizing his preference on the budget set 𝛽𝑎(𝑝).
If 𝛽𝑎(𝑝) ≠ ∅ and 𝜑𝑎(𝑝) = ∅, then consumer 𝑎 chooses his consumption plan
𝑥̃𝑎 ∈ 𝛽𝑎(𝑝), due to his own criterion. If 𝛽𝑎(𝑝) = ∅, then we assume that
𝑥̃𝑎 = 0 ∈ ℝℓ. As above, it is assumed that every inactive consumer realizes plan 𝑥̃𝑎𝑖 = 0 ∈ ℝℓ for 𝑖 > 𝑚.
Consider the Debreu economy ℇ𝑝 = (ℝℓ ,𝑃,𝐶,𝜃,𝜔). Let 𝑥𝑎∗ ∈ 𝜑𝑎(𝑝) for every 𝑎 ∈ 𝐴 as well as 𝑦𝑏∗ ∈ 𝜂𝑏(𝑝) for every 𝑏 ∈ 𝐵. If
∑𝑎∈𝐴 𝑥𝑎∗ − ∑𝑏∈𝐵𝑦𝑏∗ = 𝜔,
then the sequence
((𝑥𝑎∗)𝑎∈𝐴,(𝑦𝑏∗)𝑏∈𝐵 ,𝑝)),
where (𝑥𝑎∗)𝑎∈𝐴 ≝ (𝑥𝑎¹∗, … , 𝑥𝑎𝑚∗ ,0,0,…) and (𝑦𝑏∗)𝑏∈𝐵 ≝ (𝑦𝑏¹∗, … ,𝑦𝑏𝑛∗ ,0,0, …) is called the state of the Walras equilibrium in economy ℇ𝑝.
Extensions of the private ownership economies
To study changes in the economies, we will examine the concept of extensions of production and consumption systems respectively, as well as the economy as a whole (see also Lipieta, 2013).
Consider a quasi-production system 𝑃𝑞 = (𝐵,ℝℓ ;𝑦,𝑝) in the fixed point of time 𝑡 = 0. Assuming that system 𝑃𝑞 evolves, after a certain time in the point 𝑡 = 1, the components (see Def. 2.1) of system 𝑃𝑞 can be transformed into the components of a quasi-production system 𝑃𝑞′ = (𝐵′ ,ℝℓ′ ;𝑦′ ,𝑝′), where additionally 𝑏𝑗 =𝑏𝑗′ for every 𝑗 ∈ {1,…,max{𝑛,𝑛′}}. That will be noted by
𝑃𝑞 ⊂ 𝑃𝑞′. The quasi-production system 𝑃𝑞′ will be called the transformation of the system 𝑃𝑞 on the time interval [0,1].
If 𝑃𝑞 ⊂ 𝑃𝑞′ and an active producer 𝑏𝑗 from system 𝑃𝑞 stops his activity on the market in the observable time interval, then he will become the inactive producer in the system 𝑃𝑞′. Hence for producer 𝑏𝑗,
𝑦(𝑏𝑗) ≠ {0} and 𝑦′(𝑏𝑗) = {0}
Similarly, if an active producer 𝑏𝑗 appears in the system 𝑃𝑞′ which is the transformation of system 𝑃𝑞, then he is considered as the inactive producer in the system 𝑃𝑞 , formally
𝑦(𝑏𝑗) = {0} and 𝑦′(𝑏𝑗) ≠ {0}.
Notice that inactive agents, in fact, do not influence on actions of active producers on the market. Hence if 𝑃𝑞 ⊂ 𝑃𝑞′ , then without loss of generality we can assume that 𝑏𝑗 = 𝑏𝑗′ for every 𝑗 ∈ {max {𝑛,𝑛′} +1, … }. Hence, we assume that 𝐵 = 𝐵′.
In a given transformation of the given quasi-production system, we model the improvement in the producers’ position (compare to Def. 4. 20 in Lipieta, 2013). Namely, if 𝑃𝑞 = (𝐵,ℝℓ ;𝑦,𝑝) and 𝑃𝑞′ = (𝐵′ ,ℝℓ′ ;𝑦′ ,𝑝′) are the quasi-production systems where 𝑃𝑞 ⊂ 𝑃𝑞′, then we say that a producer
𝑏 ∈ 𝐵=𝐵′ is better off in system 𝑃𝑞′ than in system 𝑃𝑞 if and only if,
∃𝑦′𝑏 ∈ 𝑦′(𝑏) ∀𝑦𝑏 ∈ 𝑦(𝑏) 𝑝 ∘ 𝑦𝑏 < 𝑝′ ∘ 𝑦 ′𝑏 .
In the same way, as in case of quasi-production systems, we define and note down the transformation of quasi-consumption systems as well as private ownership economies with almost all inactive agents. Analogously, if 𝐶𝑞 = (𝐴,ℝℓ ,𝑃𝑟𝑒𝑓; 𝜒,𝜖,𝜀,𝑝) and (𝐴′, ℝℓ′, 𝑃𝑟𝑒𝑓′ ;𝜒′, 𝜖′, 𝜀′, 𝑝′) are the quasi-consumption systems where 𝐶𝑞 ⊂ 𝐶𝑞′ , then we say that a consumer
𝑎 ∈ 𝐴 = 𝐴′ is better off in system 𝐶 𝑞′ than in system 𝐶𝑞 if and only if,
∃𝑥′𝑎 ∈ 𝜒′(𝑎) ∀𝑥𝑎 ∈ 𝜒(𝑎): [(projℝℓ (𝑥′𝑎) ∈ 𝜒(𝑎)) ∧ (𝑥𝑎 ≺𝑎 projℝ ℓ(𝑥′𝑎))].
If ℇ𝑞 = (ℝℓ ,𝑃𝑞 ,𝐶𝑞 ,𝜃,𝜔) and ℇ′𝑞 =(ℝℓ′ ,𝑃𝑞′ ,𝐶𝑞′ ,𝜃′ ,𝜔 ′) are the private ownership economies with almost all inactive agent, where 𝑃𝑞 ⊂ 𝑃𝑞′ and
𝐶𝑞 ⊂ 𝐶𝑞′ on the same time interval [0,1], then we will say that economy ℇ𝑞′ is the transformation of economy ℇ𝑞 and note down ℇ𝑞 ⊂ ℇ𝑞′.
As it was emphasized before, to model and compare some changes in the economy under study, various kinds of extensions of adequate systems will be defined. In the below definitions, the natural projection from space
ℝℓ′ on space ℝℓ , namely mapping
projℝℓ: ℝℓ ′ ∋ (𝑥1 , … ,𝑥ℓ ′) → (𝑥1, … ,𝑥ℓ )∈ ℝℓ
for ℓ,ℓ′ ∈ {1,2, …}, ℓ ≤ ℓ′, is involved.
Let 𝑃𝑞 = (𝐵,ℝ ℓ ;y,𝑝), 𝑃𝑞′ = (𝐵′ ,ℝℓ′ ;y′, 𝑝′) be the quasi-production systems and 𝑃𝑞 ⊂ 𝑃𝑞′. Under the above notations, the following definition is formulated.
Definition 6. The quasi-production system 𝑃𝑞′ is called the cumulative extension of the quasi-production system 𝑃𝑞, in short 𝑃𝑞 ⊂𝑐 𝑃𝑞′, if
1. ℓ ≤ ℓ′,
2. 𝑝 ≤ projℝℓ(𝑝′),
3. ∀𝑏 ∈ 𝐵 𝑦(𝑏) ⊂ projℝℓ (𝑦′(𝑏)),
4. ∀𝑏 ∈ 𝐵 ∀𝑦𝑏 ∈ 𝑦(𝑏) ∃𝑦′𝑏 ∈ 𝑦′(𝑏) 𝑝 ∘ 𝑦𝑏 ≤ 𝑝′ ∘ 𝑦′𝑏.
If 𝑃𝑞 ⊂𝑐 𝑃𝑞′, then the quasi-production system 𝑃𝑞′ is said to be the strong cumulative extension of quasi-production system 𝑃𝑞 (𝑃𝑞 ⊊𝑐 𝑃𝑞′), with respect to the profit, if and only if,
∃𝑏 ∈ 𝐵 ∃𝑦′𝑏 ∈ 𝑦′(𝑏) ∀𝑦𝑏 ∈ 𝑦(𝑏) 𝑝 ∘ 𝑦𝑏 < 𝑝′ ∘ 𝑦′𝑏,
Notice that if 𝑃𝑞 ⊂𝑐 𝑃𝑞′ and ℓ=ℓ′ (then the natural projections are identity mappings), then neither new firms nor commodities appear and the old ones are not eliminated from the production process. The old technologies are still used (condition 3 by Def. 6) with non-decreasing prices (condition 2 by Def. 6), which result in not less profit (condition 4 by Def. 6). Hence, the idea of the cumulative extension of the quasi production system, where ℓ = ℓ ′ can be interpreted as the mathematical model of the Schumpeterian circular flow in the production sphere (compare to Schumpeter, 1934 and Lipieta, 2013). If
ℓ < ℓ′, then new commodities appear on the market. Moreover, if
𝑦(𝑏) = {0} and 𝑦′(𝑏) ≠ {0} for some 𝑏 ∈ 𝐵, then producer 𝑏 enters the market, if
𝑦(𝑏) ≠ {0} and 𝑦′(𝑏) = {0}, then producer 𝑏 exits the market.
The strong version of the cumulative extension of a production system with respect to its given component is defined to model and express substantial changes in the production sector (compare to Malawski, 2013).
We start now the analysis of the Schumpeterian economic development from definitions of innovations and innovative changes. The innovation is a new commodity or a new technology introduced into the economy. The innovator is the producer who introduces an innovation. Consequently, introducing a new commodity or a new technology into the production sector of an economy are called the innovative changes in the production sector (of the economy) or, simply, in that economy. To model the innovative changes in the production sector, the innovative extension of a production system is defined (compare to Lipieta, 2013).
Definition 7. The quasi-production system 𝑃𝑞′ is called the innovative extension of the quasi-production system 𝑃𝑞, in short 𝑃𝑞 ⊂𝑖 𝑃𝑞′, if
1. ℓ ≤ ℓ′,
2. ℓ = ℓ′ ⟹ ∃ 𝑏 ∈ 𝐵 ∀𝑦𝑏 ∈ 𝑦(𝑏) ∃𝑦′𝑏 ∈ 𝑦′(𝑏)\ ⋃𝑏∈𝐵 𝑦(𝑏)∶ 𝑝′ ∘ 𝑦′𝑏 > 𝑝′ ∘ 𝑦𝑏,
3. ℓ < ℓ′ ⟹ ∃ 𝑏 ∈ 𝐵 ∀𝑦𝑏 ∈ 𝑦(𝑏) ∃𝑦′𝑏 ∈𝑦′ (𝑏)\(⋃𝑏∈𝐵 (𝑦(𝑏) × {0} ×…×{0})):
𝑝′ ∘ 𝑦′𝑏 > projℝℓ(𝑝′) ∘ 𝑦𝑏
The producer satisfying condition 2 or 3 (by Def. 7) adequately, is called the innovator. If producer 𝑏 is the innovator then the vectors 𝑦′𝑏 are called (his) innovative plans.
The set of innovators will be denoted by 𝐵𝑖𝑛.
If 𝑃𝑞 ⊂𝑖 𝑃𝑞′ where ℓ = ℓ′, then innovations are reduced to the implementation of new technology into production without introducing a new commodity. Condition 2 by Definition 7 means that every innovator 𝑏 in system 𝑃𝑞′ can realize the innovative plan 𝑦′𝑏 which guarantees him a higher profit at prices determined in system 𝑃𝑞′ than any of his plan 𝑦𝑏 realized in system 𝑃𝑞. If
𝑃𝑞 ⊂𝑖 𝑃𝑞′ and ℓ < ℓ′, than a new commodity is introduced by an innovator and every innovator introduces new technology into the production sphere (condition 3 by Def. 7). The innovative plan 𝑦′𝑏 carried out by innovator 𝑏 in system 𝑃𝑞′ gives him also more profit then any plan 𝑦𝑏 realized by him in system 𝑃𝑞 but at respective prices taken from system 𝑃𝑞′. We assume, following Schumpeterian thinking, that producers’ aim is to increase the profits and it motivates them to introduce innovations. Hence, if 𝑃𝑞 ⊂𝑖 𝑃𝑞′, then every innovator in system 𝑃𝑞′ realizes such plan, which gives him a higher profit than by realizing plans feasible so far, that is one of his innovative plans. Consequently, if 𝑃𝑞′ is the production system (𝑃𝑞′ = 𝑃′), then every innovator 𝑏 realizes some plan 𝑦′𝑏 satisfying condition 2 or 3 (by Def. 7) respectively, and it has to be one of his optimal plans. Moreover, the set 𝜂′𝑏(𝑝), for every 𝑏 ∈ 𝐵𝑖𝑛, consists only of optimal plans of producer 𝑏. As a results, if ℇ𝑞 = (ℝℓ, 𝑃𝑞, 𝐶𝑞, 𝜃,𝜔) and ℇ𝑞′ = (ℝℓ′ ,𝑃𝑞′ ,𝐶𝑞′, 𝜃′ ,𝜔 ′) are the private ownership economies with almost all inactive agent, where 𝑃𝑞 ⊂𝑖 𝑃𝑞′, 𝑃𝑞′ =𝑃′ as well as ℇ𝑞 ⊂ ℇ𝑞′, then the state of equilibrium (see (2)) if existed, in economy ℇ𝑞′ contains on the coordinate proper for innovator 𝑏, one of his innovative plan which gives him maximal profit.
If 𝑃𝑞 ⊂𝑖 𝑃𝑞′ and 𝑃𝑞 is the production system (𝑃𝑞 = 𝑃), then by conditions 2 and 3 by Definition 7, it follows that
∀ 𝑏 ∈ 𝐵𝑖𝑛 ∃𝑦′𝑏 ∈ 𝑦′(𝑏) \⋃𝑏∈𝐵𝑦(𝑏): ∀𝑦𝑏 ∈ 𝑦(𝑏) 𝑝′ ∘ 𝑦′𝑏 > 𝑝′ ∘ 𝑦𝑏 if ℓ = ℓ′
or
∀ 𝑏 ∈ 𝐵𝑖𝑛 ∃𝑦′𝑏 ∈ 𝑦′(𝑏) \⋃𝑏∈𝐵(𝑦(𝑏) × {0} ×…× {0}): ∀𝑦𝑏 ∈ 𝑦(𝑏):
𝑝′ ∘ 𝑦′𝑏 > proj ℝℓ (𝑝′) ∘ 𝑦𝑏 if ℓ < ℓ′,
The above conditions mean that if 𝑃𝑞 ⊂𝑖 𝑃𝑞′ and 𝑃𝑞 is the production system, then every innovator 𝑏 in system 𝑃𝑞′ gets, by realization one of his innovative plans 𝑦′𝑏, the profit higher than profit obtained by realization any of his plans from system 𝑃𝑞 at respective prices from system 𝑃𝑞′. Hence the innovators are better off in the system 𝑃𝑞′ than in the system 𝑃𝑞 in the sense of condition (3). Hence if 𝑝 = projℝℓ (𝑝′), then the innovators are better off in the system 𝑃𝑞′ than in the system 𝑃𝑞 in the sense of condition (3).
The innovator 𝑏0, for whom
∃𝑦′𝑏0 ∈ 𝑦′(𝑏0) \⋃𝑏∈𝐵 𝑦(𝑏) ∀𝑏 ∈ 𝐵 ∀𝑦𝑏 ∈ 𝑦(𝑏) 𝑝′ ∘ 𝑦′𝑏0 > 𝑝′ ∘ 𝑦𝑏 if ℓ = ℓ′
or
∃𝑦′𝑏0 ∈ 𝑦′(𝑏0) \⋃𝑏∈𝐵 (𝑦(𝑏) × {0} ×…× {0}) ∀𝑏 ∈ 𝐵 ∀𝑦𝑏 ∈ 𝑦(𝑏)
𝑝′ ∘ 𝑦′𝑏0 > projℝℓ (𝑝′) ∘ 𝑦𝑏 if ℓ < ℓ′.
is called the leading innovator, the market leader or shortly the leader. If
𝑃𝑞 ⊂𝑖 𝑃𝑞′ as well as one of the above condition is satisfied, then there is at least one innovator 𝑏 in system 𝑃𝑞′ who gains, by realization one of his innovative plans 𝑦′𝑏 , the profit higher than profits of all producers from system 𝑃𝑞, determined at respective prices taken from system 𝑃𝑞′.
The leaders can also appear in quasi-production systems but if there is a producer in system 𝑃𝑞 for whom the maximal profit does not exist, then no leader will appear in system 𝑃𝑞′. If 𝑃𝑞′ is the production system (𝑃𝑞′ = 𝑃′), then there is at least one market leader in system 𝑃𝑞′.
Let us notice that if the quasi-production system 𝑃𝑞′ is the cumulative extension of the production system 𝑃𝑞 (𝑃𝑞 ⊊𝑐 𝑃𝑞′) with respect to the profit, then 𝑃𝑞′ can be also the innovative extension of 𝑃𝑞 (𝑃𝑞 ⊂𝑖 𝑃𝑞′).
Similarly, and for the same reasons as in case of the production sector, we define extensions of the quasi-consumption system. Let 𝐶𝑞 = (𝐴,ℝℓ ,𝑃𝑟𝑒𝑓; 𝜒,𝑒,𝜀,𝑝), 𝐶𝑞′ = (𝐴′, ℝℓ′, 𝑃𝑟𝑒𝑓′ ;𝜒′, 𝑒′, 𝜀′, 𝑝′) be the quasi-consumption systems and 𝐶𝑞 ⊂ 𝐶𝑞′.
Definition 8. The quasi-consumption system 𝐶𝑞′ is said to be the cumulative extension of the quasi-consumption system 𝐶𝑞, in short 𝐶𝑞 ⊂𝑐 𝐶𝑞′, if
1. ℓ ≤ ℓ′,
2. 𝑝 ≤ projℝℓ (𝑝′),
3. 𝐴 = 𝐴′,
4. ∀𝑎 ∈ 𝐴 𝜒(𝑎) ⊂ projℝℓ (𝜒′(𝑎)),
5. ∀𝑎 ∈ 𝐴 𝑒(𝑎) ≤ projℝℓ (𝑒′(𝑎)),
6. ∀𝑎 ∈ 𝐴 𝜀(𝑎) ⊂ projℝℓ (𝜀′(𝑎)),
7. ∀𝑎 ∈ 𝐴 ∀𝑥𝑎 ∈ 𝜒(𝑎) ∃𝑥′𝑎 ∈𝜒′(𝑎) projℝℓ (𝑥′𝑎) ∈ 𝜒(𝑎) ∧ 𝑥𝑎 ≼𝑎 projℝℓ(𝑥′𝑎).
The cumulative extension 𝐶𝑞 ′ is the strong cumulative extension (𝐶𝑞 ⊊𝑐 𝐶𝑞′) of the quasi-consumption system 𝐶𝑞, with respect to the demand ⟺
∃𝑎 ∈ 𝐴 ∃𝑥′𝑎 ∈ 𝜒′(𝑎) [(𝑝𝑟𝑜𝑗ℝℓ(𝑥′𝑎) ∈ 𝜒(𝑎)) ∧ (∀𝑥𝑎 ∈ 𝜒(𝑎) 𝑥𝑎 ≺𝑎 projℝℓ(𝑥′𝑎))].
The complete definition of the strong cumulative extensions of the quasi-consumption system due to other criterions, the reader can find, for instance in (Malawski, 2013).
Let ℇ𝑞 = (ℝℓ ,𝑃𝑞, 𝐶𝑞, 𝜃, 𝜔) and ℇ𝑞′ = (ℝℓ′, 𝑃𝑞′, 𝐶𝑞′, 𝜃′, 𝜔′) be the private ownership economies with almost all inactive agents. Let ℇ𝑞 ⊂ ℇ𝑞′. On the basis of the above definitions, we put the following:
Definition 9. The economy ℇ𝑞′ is said to be the cumulative extension of the
ℇ𝑞, in short ℇ𝑞 ⊂𝑐 ℇ𝑞′, if
1. 𝑃𝑞 ⊂𝑐 𝑃𝑞′,
2. 𝐶𝑞 ⊂𝑐 𝐶𝑞′,
3. 𝜔 ≤ 𝜔′.
If ℇ𝑞 ⊂𝑐 ℇ𝑞′ and 𝑃𝑞 ⊊𝑐 𝑃𝑞′ or 𝐶𝑞 ⊊𝑐 𝐶𝑞′, then economy ℇ𝑞′ is said to be the strong cumulative extension of economy ℇ𝑞, in short ℇ𝑞 ⊊𝑐 ℇ𝑞′.
If 𝑃𝑞 ⊂𝑖 𝑃𝑞′ then economy ℇ𝑞′ is the innovative extension of economy ℇ𝑞, in short ℇ𝑞 ⊂𝑖 ℇ𝑞.
Mechanisms connected to evolutions of the private ownership economies
In this part of the paper, some definitions useful for modeling the structure of Schumpeterian evolution mechanisms will be formulated.
Let 𝐸 ≠ ∅ be the set of environments, namely elements that constrain the situation of economic agents (see Hurwicz, Reiter, 2006; Jordan 1982). The set of desired outcomes (the outcome sets) is denoted by 𝑍 (𝑍 ≠ ∅). It is assumed that the economic agents can communicate by sending and retrieving messages that are necessary for achieving goals.
Definition 10. (Hurwicz, Reiter, 2006). The triple 𝛤 = (𝑀,𝜇,ℎ), where
- 𝑀 ≠ ∅ is the message space,
- 𝜇: 𝐸 → 𝑀 is the message correspondence,
- ℎ: 𝑀 → 𝑍 is the outcome function
is called the economic mechanism.
It is said that an economic mechanism 𝛤 = (𝑀,𝜇,ℎ) realizes the goal function (or correspondence) 𝐹: 𝐸 → 𝑍 if
∀𝑒 ∈ 𝐸 ℎ(𝜇(𝑒)) ⊂ 𝐹(𝑒).
Now, we will distinguish two classes of mechanisms, price and qualitative mechanisms.
Definition 11 (Lipieta, 2013). An economic mechanism, in which the prices of commodities are elements of the message space which will be called the price mechanism.
An economic mechanism, in the consequence of which the position of at least one agent from a subset of the set of all agents will be better off in the sense of conditions (3) and (4), without making the position of the rest of the agents from the subset worse off, will be called the qualitative mechanism with respect to this subset.
Now let us focus on the structure of evolution of the economy under study. At the beginning, we consider the Debreu economy ℇ𝑝 = (ℝℓ ,𝑃,𝐶,𝜃,𝜔) in which a state of equilibrium exists. According to Schumpeterian ideas (see Schumpeter, 1934) economy ℇ𝑝 evolves for a certain time, in the direction to its modified form that is its innovative extension ℇ𝑝′ =(ℝℓ′, 𝑃′, 𝐶′, 𝜃′, 𝜔′ ). Hence ℇ𝑝 ⊂𝑖 ℇ𝑝′ . The final economy ℇ𝑝′ should also be the Debreu economy in equilibrium. In the meantime, some agents might enter or exit the economy, the producers can change their technologies, some innovations can be introduced into the market, the consumption sets and the budget sets might be verified as well as the producers’ and consumers’ optimal plans can be changed. In some cases, the producers do not maximize their profits or the consumers do not manage to maximize their preferences, etc. All of that becomes the basis for our modeling.
It should be emphasized that the expected increase in the profits motivates innovators to modifying their technologies.
Let ℇ𝑞 be the private ownership economy. By ℇ𝑞′(𝑡), for every 𝑡 ∈ (0,1] we will denote the transformation of the economy ℇ𝑞 at point of time 𝑡, defined in the same way as for 𝑡 = 1. The above dependence will be denotes as above, namely ℇ𝑞 ⊂ ℇ𝑞′(𝑡). The set 𝔼𝑞(ℇ𝑞) stands for the set of all possible transformations of economy ℇ𝑞 on the time interval (0,1], namely
𝔼𝑞(ℇ𝑞) = {ℇ𝑞(𝑡): ℇ𝑞 ⊂ ℇ𝑞′(𝑡) ∧ 𝑡 ∈ (0,1]}.
Let points of time 𝑡0, 𝑡1, … ,𝑡𝑆 satisfying 0 = 𝑡0 < 𝑡1 < ⋯ <𝑡𝑆 = 1 for some
𝑆 ∈ {1,2,…} be all the points of changes in economic activity of producers or consumers.
Definition 12. The mapping 𝑇: [0,1] → 𝔼𝑞(ℇ𝑞) satisfying
𝑇(0) = ℇ𝑞, 𝑇(1) = ℇ𝑞′(1) = ℇ𝑞′, 𝑇(𝑡) = ℇ𝑞′(𝑡𝑠) for 𝑡 ∈ [𝑡𝑠−1, 𝑡𝑠 ) for 𝑠 ∈ {1,2, … ,𝑆}
is called the transition from the economy ℇ𝑞 to the economy ℇ𝑞′.
If additionally ℇ𝑞 ⊂𝑖 ℇ𝑞′ then transition 𝑇 is called the innovative evolution of economy ℇ𝑞.
The interval [0,1] is interpreted as the time of evolution of economy ℇ𝑞 to economy ℇ𝑞′.
Theorem 1 If ℇ𝑞 and ℇ𝑞′ are private ownership economies with almost all inactive agents, then the transition 𝑇 from economy ℇ𝑞 to economy ℇ𝑞′, is the price mechanism.
Proof. Let 𝐾 = {𝑎1, 𝑏1, 𝑎2, 𝑏2,…} be the set of agents. The environment of every agent 𝑘 ∈ 𝐾 in this situation is determined by the characteristics of that agent in economy ℇ𝑞. Hence it is of the form:
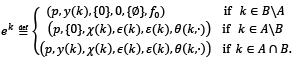
Hence the set of environments 𝐸𝑘 of every agent 𝑘 and the set of environments 𝐸 are given by
𝐸𝑘 = ℝℓ × 𝑃(ℝℓ) × 𝑃(ℝℓ) × ℝℓ ×𝑃(ℝ2ℓ) × ℱ(𝐵,[0,1]),
𝐸 ≝ 𝐸𝑘1 × 𝐸 𝑘2 ×… ,
where
ℱ(𝐵, [0,1]) = {𝑓:𝐵→ [0,1]}, 𝑓0 ∈ ℱ(𝐵, [0,1]),𝑓0 ≡ 0
Put
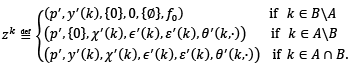
and consequently
𝑍𝑘 = ℝℓ′ × 𝑃(ℝℓ′) × 𝑃(ℝℓ′) × ℝℓ′ × 𝑃(ℝ2ℓ′) × ℱ(𝐵, [0,1]).
The logic structure of action of economy ℇ𝑞 implies that
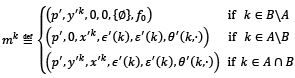
as well as 𝜇𝑘: 𝐸𝑘 → 𝑀, for every agent 𝑘 ∈ 𝐾, is given by
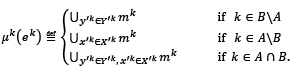
Now we get that
𝑀𝑘 = ℝℓ′ × ℝℓ′ × ℝℓ′ × ℝℓ′ × ℝ2ℓ′ × ℱ(𝐵, [0,1]), 𝑀 ≝ 𝑀𝑘1 × 𝑀𝑘2 ×….
Defining message correspondence 𝜇: 𝐸 → 𝑀 by the rule
𝜇(𝑒) ≝ 𝑋𝑘∈𝐾𝜇𝑘(𝑒𝑘)
and the outcome function ℎ: 𝑀 → 𝑍
ℎ: 𝑀 → 𝑍, ℎ ≝ 𝑖𝑑𝑀,
we get that the transition from economy ℇ𝑞 to economy ℇ𝑞′ is the privacy preserving price mechanism realizing the goal correspondence
𝐹: 𝐸 ∋ (𝑒1, 𝑒2 , …) → {(𝑧1, 𝑧2 , …)} ∈ 𝑍,
with the set of outcomes 𝑍. The components of the environments {𝑧𝑘}𝑘∈𝐾 form the economy ℇ𝑞′ which gives the results.
A similar reasoning leads us to the theorems which give the conditions sufficient for the price mechanism 𝑇 to be a suitable qualitative mechanism.
Theorem 2. Let ℇ𝑞 and ℇ𝑞′ be the private ownership economies with almost all inactive agents, ℇ𝑞 ⊂ ℇ𝑞′.
1. If 𝑃𝑞 ⊂𝑖 𝑃𝑞′, 𝑝=projℝℓ (𝑝′) and 𝑃𝑞′ = 𝑃′, then the price mechanism 𝑇 is also the qualitative mechanism with respect to the set of innovators,
2. If 𝑃𝑞 ⊊𝑐 𝑃𝑞′ with respect to the profit and 𝑃𝑞′ = 𝑃′, then the price mechanism 𝑇 is the qualitative mechanism with respect to the set of all producers,
3. If 𝐶𝑞 ⊊𝑐 𝐶𝑞′ with respect to the demand and 𝐶𝑞′ =𝐶′ , then the price mechanism 𝑇 is the qualitative mechanism with respect to the set of all consumers.
On the basis of theorems 1 and 2 we get the following:
Theorem 3. Let ℇ𝑞, ℇ𝑞′ be the private ownership economies with almost all inactive agents, ℇ𝑞 ⊂ ℇ𝑞′ as well as ℇ𝑞′ = ℇ𝑝′.
1. If ℇ𝑞 ⊊𝑐 ℇ𝑞′, where 𝐶𝑞 ⊊𝑐 𝐶𝑞′ with respect to the demand or 𝑃𝑞 ⊊𝑐 𝑃𝑞′ with respect to the profit, then the price mechanism 𝑇 is also the qualitative mechanism with respect to the set of all agents.
2. If ℇ𝑞 ⊂𝑖 ℇ𝑞′ and 𝑝=projℝℓ (𝑝′), then the price mechanism 𝑇 is also the qualitative mechanism with respect to the set of innovators.
3. If ℇ𝑞 ⊂𝑖 ℇ𝑞′, 𝑝=projℝℓ (𝑝′) as well as 𝐶𝑞 ⊂𝑐 𝐶𝑞′, then the price mechanism 𝑇 is also the qualitative mechanism with respect to the set consisted of consumers and innovators.
Comparative analysis of mechanisms of evolutions of the Debreu economy
To compare possible innovative evolutions of the Debreu economy, we define the index of innovativeness of a possible transformation of the economy under study. It relies on comparing states of equilibrium in the adequate economies.
Let ℇ𝑞 = (ℝℓ, 𝑃𝑞, 𝐶𝑞, 𝜃, 𝜔) and ℇ𝑞′ = (ℝℓ′, 𝑃𝑞′, 𝐶𝑞′, 𝜃′, 𝜔′) be the private ownership economies with almost all inactive agents. First we determine the distance between the allocations in economies ℇ𝑞 and ℇ𝑞′. Let us recall that if a producer 𝑏𝑗, for 𝑗 ∈ {1,2,…,𝑛}, will exit the market in point of time 𝑡 ∈ (0,1], then 𝑦′(𝑏𝑗) = {0} and consequently 𝑦′𝑏𝑗 = 0 ∈ ℝ ℓ′. Similarly, if a producer 𝑏𝑗 , for 𝑗 > 𝑛, enter the market in point 𝑡 ∈ (0,1], then we put 𝑦𝑏𝑗 = 0. Under the above assumptions, for 𝑗 ∈ 𝐽 ≝ {1,2, … ,𝑚𝑎𝑥{𝑛,𝑛′}} the distance between vectors 𝑦𝑏𝑗 and 𝑦′𝑏𝑗, is defined b
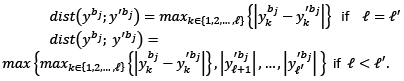
In the same way, the distance between consumption plans 𝑥𝑎𝑖 and 𝑥′𝑎𝑖 for every 𝑖 ∈ 𝐼 ≝ {1,2, … , 𝑚𝑎𝑥{𝑚,𝑚′}} is defined.
On the basis of the above, we define the index which helps to compare the innovativeness of different transformations of the initial economy. Following Schumpeterian thinking, we assume that both: the initial and final economies are the Debreu economies (ℇ𝑞 = ℇ𝑝 ,ℇ𝑞′ = ℇ𝑝′) as well as ℇ𝑝 ⊂𝑖 ℇ𝑝′. Let ((𝑥𝑎∗)𝑎∈𝐴 ,(𝑦𝑏∗)𝑏∈𝐵 ,𝑝) and ((𝑥′𝑎∗)𝑎∈𝐴 ,(𝑦′𝑏∗)𝑏∈𝐵 ,𝑝′) be states of equilibrium in the economies, adequately ℇ𝑝 and ℇ𝑝′.
The distance between two states is equal:
𝑑𝑖𝑠𝑡(((𝑥𝑎∗)𝑎∈𝐴 ,(𝑦𝑏∗)𝑏∈𝐵); ((𝑥′𝑎∗)𝑎∈𝐴 ,(𝑦′𝑏∗)𝑏∈𝐵)) ≝
𝑚𝑎𝑥{𝑚𝑎𝑥{𝑑𝑖𝑠𝑡(𝑦𝑏𝑗∗ ; 𝑦′𝑏𝑗∗): 𝑗 ∈ 𝐽}; 𝑚𝑎𝑥{𝑑𝑖𝑠𝑡(𝑥𝑎𝑖∗ ;𝑥′𝑎𝑖∗): 𝑖 ∈ 𝐼}}
The number (7) is called the index of innovativeness of the economy ℇ𝑞 ′ with the realized allocation ((𝑥′𝑎∗)𝑎∈𝐴 ,(𝑦′𝑏∗)𝑏∈𝐵). It measures the highest difference between the quantities of commodities in the agents’ plans of actions in times 𝑡 = 0 and 𝑡 = 1. Consequently, the above defined index of innovativeness shows the biggest change introduced to the economy under study on the given time interval. Let us emphasize that the level of the index of innovativeness of the economy ℇ𝑝′ depends not only on the initial economy but also on the realized allocation. If the designer of economic activity aims at inducing or increasing the innovative activities on market, then he will intend to establish the state of equilibrium with the higher level of the index of innovativeness rather than with the smaller one, especially if the innovators are better off (see (3)) in the economy ℇ𝑝′ than in the initial economy ℇp.
It may happen that in the final economy ℇ𝑝′ there are at least two different states of equilibrium with the same index of innovativeness. Then it seems to be “very Schumpeterian” that the designer will tend to establish a “better” state of equilibrium. This is the problem under study in the next part of the paper.
Comparative analysis of mechanisms of equilibrium in the Debreu economy
As was emphasized earlier, the final stage of Schumpeterian economic development is moving the system to a new stationary state, where previous innovations have been absorbed in the equilibrated system (see for instance Andersen, 2009). If, for some 𝑠 ∈ {1,2, … ,𝑆}, ℇ𝑞 ⊂𝑖 ℇ𝑞′ (𝑡𝑠) where ℇ𝑞′(𝑡𝑠) is the Debreu economy, then at time 𝑡𝑠 , the adapting mechanisms will start working in the economy ℇ𝑞′(𝑡𝑠) until any producer does not change his activity on the market. If any producer introduces innovative changes, then it means that innovative evolution of economy ℇ𝑞 is still working. The innovative evolution will be stopped when every producer will be satisfied with his profit and the consumers will adopt the innovations into consumptions plans. Hence if ℇ𝑞 ⊂𝑖 ℇ𝑞′ and the producers do not change their plans of action as well as ℇ𝑞′ is the Debreu economy (ℇ𝑞′ = ℇ𝑝′), the adopting procedures start working.
Now we face a challenge to model the second type of mechanism whose output is a state of equilibrium in the given economy. This type of mechanism was defined in Lipieta (2013) but for an economy with a finite number of agents. The following theorem is proved in the same way as Theorem 4. 1 in Lipieta (2013).
Theorem 4. Let ℇ𝑝 = (ℝℓ ,𝑃,𝐶,𝜃,𝜔) be the Debreu economy and
𝑍 = {((𝑥𝑎∗)𝑎∈𝐴 ,(𝑦𝑏∗)𝑏∈𝐵): ∃𝑝 ∈ ℝℓ ∀𝑎 ∈ 𝐴,𝑏 ∈ 𝐵 𝑥𝑎∗ ∈𝜑𝑎(𝑝) ,𝑦𝑏∗ ∈ 𝜂𝑏(𝑝)
∧∑𝑎∈𝐴𝑥𝑎∗ − ∑𝑏∈𝐵𝑦𝑏∗ = 𝜔}.
If the set 𝑍 is not empty, then the components of economy ℇ𝑝 form the economic mechanism with 𝑍 as the set of outcomes.
Proof. Let 𝐾 = {𝑎1 ,𝑏1 ,𝑎2 ,𝑏2 ,…} be the set of agents. The environment of agent 𝑘∈𝐾 is of the form (5), the set of environments 𝐸𝑘 of every agent 𝑘 ∈ 𝐾 as well as the set of environments 𝐸 are of the form (6). Define
- 𝑀 = {m = (𝑝,𝑥𝑎¹ ,𝑦𝑏¹ ,𝑥𝑎2 ,𝑦𝑏2 ,…)∈ ℝℓ × 𝑋𝑎¹ × 𝑌𝑏¹ ×…∶
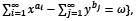
- 𝜇(𝑒) = 𝜇(𝑒𝑎¹ ,𝑒𝑏¹ ,𝑒𝑎2 ,𝑒𝑏2 ,…) ≝ ⋂𝑘∈𝐾 𝜇𝑘(𝑒𝑘) where
𝜇𝑘: 𝐸𝑘 → 𝑀 is the message correspondence of agent 𝑘∈𝐾 such that
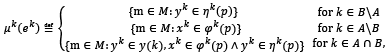
- ℎ: 𝑀 → 𝑍, ℎ(𝑝, 𝑥𝑎¹, 𝑦𝑏¹, 𝑥𝑎2 ,𝑦𝑏2 ,… ) ≝ (𝑥𝑎¹ , … , 𝑥𝑎𝑚, 𝑦𝑏¹ , … , 𝑦𝑏𝑛).
By the above definitions, we immediately get that the structure 𝛤 = (𝑀,𝜇,ℎ), is the price mechanism realizing the goal correspondence
𝐹: 𝐸 ∋ (𝑒𝑘¹ ,𝑒𝑘2 , …) → (𝑥𝑎¹∗ , … , 𝑥𝑎𝑚∗ , 𝑦𝑏¹∗, … , 𝑦𝑏𝑛∗) ∈ 𝑍
The mechanism defined in Theorem 4 will be called the mechanism of equilibrium in economy ℇ𝑝 or the adopting mechanism. As we see, if there is equilibrium in the given Debreu economy, then comparing mechanisms of equilibrium in this economy refers to comparing its feasible states of equilibrium in this economy, which are the output of some mechanism of Schumpeterian evolution studied earlier.
DISCUSSION
Let ℇ𝑝 = (ℝℓ, 𝑃𝑞, 𝐶𝑞, 𝜃, 𝜔) be the Debreu economy where two states of equilibrium (see (2)) are feasible, namely
𝑅 ̃ ≝ ((𝑥̃𝑎∗)𝑎∈𝐴 ,(𝑦̃𝑏∗)𝑏∈𝐵 ,𝑝̃) and 𝑅 ̃ ≝ ((𝑥̃𝑎∗) 𝑎∈𝐴 ,(𝑦̃𝑏∗)𝑏∈𝐵 ,𝑝̃).
Now the problem under study is to define a criterion to enable comparing these two sequences in the context of improving positions of the economic agents taking part in the market activities in the meaning of conditions (3) and (4) or under improvement of the position of the economy as a whole. The term: improvement of the position of the economy will be defined later.
First, some basic properties of states of equilibrium or quasi-equilibrium in the private ownership economy will be presented. Assume first that 𝑝 ̃ = 𝑝. Then
𝑥𝑎𝑖∗ ∼𝑖 𝑥̃𝑎𝑖∗ for every 𝑖 ∈ {1, … ,𝑚} and 𝑝 ∘ 𝑦𝑏𝑗∗ = 𝑝̃ ∘ 𝑦̃𝑏𝑗∗ for every 𝑗 ∈ {1,…,𝑛}.
It means that the positions of every economic agent in the sense of conditions (3) and (4) are not changed. If 𝑝̃= 𝑘∙𝑝 for 𝑘 > 1, then also
𝑥𝑎𝑖∗ ∼𝑖 𝑥̃𝑎𝑖∗ for every 𝑖 ∈ {1, … ,𝑚}
but
𝑝 ∘ 𝑦𝑏𝑗∗ > 0 ⟹ 𝑝 ∘ 𝑦𝑏𝑗∗ < 𝑝̃ ∘ 𝑦̃𝑏𝑗∗ for every 𝑗 ∈ {1, … ,𝑛}
as well as
𝑝 ∘ 𝑦𝑏𝑗∗ < 0 ⟹ 𝑝 ∘ 𝑦𝑏𝑗∗ > 𝑝̃ ∘ 𝑦̃𝑏𝑗∗ for every 𝑗 ∈ {1, … ,𝑛}
As we see, if the prices are proportionally higher in the sequence 𝑅 ̃ than in sequence 𝑅 (see (8)) then some economic agents can be better off (see (3)) while some of them can be worse off in the state of economy of the form 𝑅 ̃ in comparing to the state 𝑅. The same can appear if vectors 𝑝̃ and 𝑝 are diametrically different. So, in many cases, the positions of some economic agents are improved while some of them not.
By this reason, we focus on ordering the feasible states of equilibrium in the Debreu economy under the other criterion. Let ℇ𝑝 = (ℝℓ ,𝑃𝑞 ,𝐶𝑞 ,𝜃,𝜔) be the Debreu economy where two states of equilibrium: 𝑅 and 𝑅 ̃ , are feasible (see (2)). Notice firstly that
𝑝 ∘ (∑𝑎∈𝐴𝑥𝑎∗) = 𝑝 ∘ 𝜔 + (𝑝 ∘ ∑𝑏∈𝐵 𝑦𝑏∗).
The number
𝑤 ≝ 𝑝 ∘ (∑𝑎∈𝐴 𝑥𝑎∗)
can be interpreted as the total wealth of economy ℇ𝑝 at state 𝑅 (see (8)), while the number
𝑊 = 𝑤 − 𝑝 ∘ 𝜔
is the increment of the total wealth of the economy ℇ𝑝 at state 𝑅. We can say that Debreu economy ℇ𝑝 improved its position at state 𝑅 if 𝑊 > 0.
The increment of the total wealth of the economy ℇ𝑝 can be obtained, among others, by activity of innovators on the market.
Analogously, we define numbers 𝑤̃ and 𝑊 ̃ at state 𝑅 ̃ (see (8), (10) and (11)). By (9) we get that if
𝑝 ∘ ∑𝑏∈𝐵𝑦𝑏∗ > 𝑝̃ ∘ ∑𝑏∈𝐵 𝑦̃𝑏∗ ⟹ 𝑊 > 𝑊
On the basis of property (12) we say that the state 𝑅 ̃ is more beneficial (more preferable) for economy ℇ𝑝 than state 𝑅, shortly 𝑅 ≺ 𝑅 ̃ , if and only if increment of the total wealth of that economy at state 𝑅 ̃ is higher than at state 𝑅, formally
𝑅 ≺ 𝑅 ̃ ⟺ 𝑊 < 𝑊 ̃ .
Hence if 𝑅, 𝑅 ̃ are two feasible states of equilibrium in economy ℇ𝑝 (see (8)) and 𝑅 ≺ 𝑅 ̃ , then the designer of economic activity in economy ℇ𝑝 should make producers and consumers realize their optimal plans from sequence 𝑅 ̃rather than from sequence 𝑅. Recall that innovators realize their innovative plans and that is why they are elements of the sequence adequately 𝑅 or 𝑅 ̃ (see (8)). Hence the sufficiently large number of innovators allows, in many cases, for the gain of an increment of the total wealth of the Debreu economy at a possibly high level.
Analogously, we say that states 𝑅̃ and 𝑅 are equally beneficial (indifferent), in short 𝑅 ̃ ∼𝑅, if the increments of the total wealth of that economy at state 𝑅 and at state 𝑅 ̃ are equal, precisely
𝑅 ̃ ∼𝑅 ⟺ 𝑊 = 𝑊 ̃ .
On the basis of the above, we say that state 𝑅 ̃ is at least preferred as state 𝑅 if it is more beneficial or indifferent. Formally,
𝑅 ≼ 𝑅 ̃ ⟺ 𝑅 ≺ 𝑅 ̃ ∨ 𝑅 ∼ 𝑅 ̃
It is easy to check that relation ≼ ⊂ (ℝℓ)2(𝑚+𝑛+1) is reflexive, transitive and complete. Hence the relation defined in (13) is the preference relation in the set of all feasible states of equilibrium of economy ℇ𝑝.
Let ℇp = (ℝℓ ,𝑃, 𝐶, 𝜃, 𝜔) and ℇ ̃ p = (ℝℓ, 𝑃̃, 𝐶 ̃ , 𝜃, 𝜔) be two Debreu economies different only in price system. Let 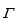 and
and 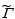 be the mechanisms of equilibrium respectively in economies ℇp and
be the mechanisms of equilibrium respectively in economies ℇp and
Taking all the above into consideration we define
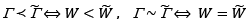
and consequently
Let:
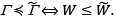
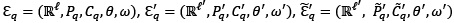
be the Debreu economies and ℇ𝑞 ⊂𝑖 ℇ𝑞′ and ℇ𝑞 ⊂𝑖 ℇ ̃ 𝑞′ on time interval [0,1]. We can implement the results of that part of the paper to the economies ℇ𝑞′ and ℇ ̃ 𝑞′. On the basis of the above results, the designer can order the adopting mechanisms in the set of possible economies ℇ𝑞′ for which ℇ𝑞 ⊂𝑖 ℇ𝑞′, which differ only in price system, formally in the set:
𝔼𝑞 (ℇ𝑞 ;ℇ𝑞′ ) ≝ 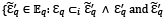 differ only in price system}.
differ only in price system}.
The internal structure of this domain can be the research object of the future studies.
CONCLUSION
In contrast to some neo-Schumpeterian studies, where two kinds of mechanisms in the framework of Schumpeterian evolution, namely the innovative evolution mechanism as well as the adopting mechanism were only indicated and considered verbally, we distinguished and modeled them in a general and rigorous manner. Moreover, some of these mechanisms appear to be qualitative ones, which reveal their complex structure and can be a promising starting point for further analysis of these types of mechanisms. We have also precisely explained the motivations of innovators and the reason for which the innovations are adopted into the producers’ and consumers’ plans of action and, in consequence, their influence on the components of states of equilibrium.
The criteria for comparing the two types of modeled mechanisms, based on some properties of the adequate set of outcomes, also were presented. They enable, among others, the measurement of the innovativeness of the processes under study, as well as the comparison of the feasible states of equilibrium in the modified economies. All this can be the basis for further research. Especially, the role of market leaders in the evolutionary processes seems to be worth studying as well as examining the “best” or at least the “good enough” mechanisms among the mechanisms presented in the paper, from the point of view of designers, consumers or innovators, respectively.
Acknowledgment
This work is partially supported by the National Science Centre in Poland, GRANT 2014/13/B/HS4/03348.
References
Andersen, E. S. (2009). Schumpeter’s Evolutionary Economics. London: London Anthem Press.
Ciałowicz, B. , & Malawski, A. (2011). The role of banks in the Schumpeterian innovative evolution - an axiomatic set-up. In A. Pyka, F. Derengowski & M. da Graca (Eds. ), Catching Up, Spillovers and Innovations Networks in a Schumpeterian Perspective (pp. 31-58). New York: Springer.
Debreu, G. (1959). Theory of Value. New York: Wiley.
Hanusch, H. , & Pyka, A. (2007). Schumpeter, Joseph Alois (1883-1950). In H. Hanusch & A. Pyka (Eds. ), Elgar Companion on Neo-Schumpeterian Economics (pp. 19-27). Cheltenham: Edward Elgar.
Hurwicz, L. , & Reiter, S. (2006). Designing Economic Mechanism. New York: Cambridge University Press.
Jordan, J. (1982). The competitive allocation process is informationally efficient uniquely. Journal of Economic Theory, 28, 1-18.
Lipieta, A. (2013). Mechanisms of Schumpeterian Evolution. In A. Malawski (Ed. ). Innovative Economy as the Object Investigation in Theoretical Economics (pp. 94-119). Cracow: Cracow University of Economics Press.
Lipieta, A. , & Malawski, A. (2016). Price versus quality competition: In search for Schumpeterian evolution mechanisms. Journal of Evolutionary Economics, 26, (pp. 1137-1171).
Malawski, A. (2005). A dynamical system approach to the Arrow-Debreu theory of general equilibrium. The Proceedings of the 9th World Multi-Conference on Systemics, Cybernetics and Informatics (pp. 434-439). Orlando Florida.
Malawski, A. (2008). Distributive justice and Schumpeterian innovative evolution - an axiomatic approach in the context of social cohesion. In A. Ostasiewicz (Ed. ), Proceedings of the Fourth International Conference on Quality of Life Improvement through Social Cohesion, (pp. 80-98). Wrocław: Wrocław University of Economics.
Malawski, A. , & Woerter, M. (2006). Diversity structure of the Schumpeterian evolution. An axiomatic approach. Arbeitspapiere/Working Papers of the Swiss Institute for Business Cycle Research, No. 153, Zurich.
Malawski, A. (Ed. ) (2013). Innovative Economy as the Object Investigation in Theoretical Economics. Cracow: Cracow University of Economics Press.
Schumpeter, J. A. (1934). The Theory of Economic Development. Cambridge, MA: Harvard University Press.
Biographical notes
Agnieszka Lipieta, Ph. D. is an Assistant Professor at the Cracow University of Economics, Department of Mathematics. Her main research areas include the theory of general equilibrium, the Schumpeter’s theory of economic growth as well as the designing economic mechanisms.
Andrzej Malawski was a Professor at the Cracow University of Economics, Head of Department of Mathematics. His main research areas included the Schumpeter’s theory of economic growth, the theory of general equilibrium, the theory of economic systems.





